干扰筛选是通过成对的差异检测进行的：测量有干扰物质和无干扰物质的样品，并确定被测量的浓度差异。

对于干扰筛选，潜在的药物干扰物质的评估浓度是治疗性药物治疗过程中观察到的最高值的三倍。对于内源性物质，推荐的浓度变化更大。详情见EP37表1（关于潜在的干扰药物）和表2（关于潜在的内源性干扰物质）。

将观察到的差异与预先确定的可允许的差异δ进行比较。当观察到的差异不超过δ时，该差异是不重要的，无需进行额外的检测。显示有临床意义的差异的物质被认为是干扰物质，要进行额外的评估，以确定干扰物质浓度、被测量水平和干扰程度之间的关系（见第六章）。

注：没有一个实用的干扰检测策略可以识别所有的干扰物质。一些干扰物质（如药物代谢物）在干扰筛选研究中可能无法被识别。其他物质可能被错误地归类为干扰物质（例如，该物质的形式并不代表自然发生的形式）。干扰筛选研究提供了一个标准化的评估，补充了对实际患者标本的研究。

干扰筛选的一些局限性包括：

➤ 添加到标本中的化合物的特性可能与体内自然循环的化合物的特性不同；

➤ 在检测的干扰物质和被测量的浓度下，不同的干扰效应可能会抵消。例如，血红蛋白（干扰物质）应始终在一个以上的胆红素（被测量）浓度下进行干扰评估；

➤ 在全血标本中添加干扰物质可能会导致溶血、液体分配差异或其他问题；

➤ 由于干扰物质的可溶性或准备基础混样时的其他物理限制等因素，在体液中添加干扰物质以检测高值的推荐检测水平（三倍于临床观察的最高值）可能是不可能的；

来自真实患者标本的数据可与加标样品的数据结合使用，以帮助确定真正的干扰。

《干扰检测中使用的被测量浓度》中给出了许多常见被测量的推荐检测浓度。每个潜在的干扰物质都应该在两个被测量浓度下进行检测，最好是在医学决定点上进行。当这不实际时，《干扰检测中使用的被测量浓度》指出了首选的检测浓度。当不遵循EP07中的程序时，应提供所用方案的理由。

在得出某种物质有干扰或无干扰的结论之前，评估者应确保研究的设计是适当的。需要有足够数量的测量（复测），以便在进行试验时有足够的能力检测出有临床意义的干扰，并有足够的置信水平来确认是否存在差异。

本系列文章中用于设计研究的统计方法被称为「假设检验」。评估者事先决定在患者结果中多少差异是有临床意义的。这个可允许的差异量被称为干扰极限。统计检验包括一个零假设（没有干扰）和一个备选假设（有干扰）。

这种统计检测是以预先确定的统计功效（1-β）和置信水平（1-α）水平进行的。

注：虽然有一个隐含的假设和相关的α和β误差指导本研究的标本量，但分析并不涉及假设检验。也就是说，没有进行与临界值的比较或对P值的审查。相反，分析涉及将平均差异点估计值与允许的差异进行比较。

为获得所需的信心和统计功效所需的复测次数取决于被检测的统计假设：

➤ 当替代假设没有说明干扰物质的方向（正或负）时，可使用双侧检验。例如，在肌酐检测中，当样品中存在浓度为14.4 mg/dL的阿米卡星干扰物质时，在1.0 mg/dL的肌酐浓度下，观察到± 0.2 mg/dL的差异；

➤ 当干扰方向（阳性或阴性）包含在备选假设中时，就会使用单侧检验。例如，在肌酐检测中，当样品中存在浓度为14.4 mg/dL的阿米卡星干扰物质时，观察到+ 0.2 mg/dL的差异，而肌酐浓度为1.0 mg/dL。

接下来的文章将解释如何确定所需的复测次数，以确保使用最小复测次数的研究具有适当的统计功效。当计算出的复测次数少于5次时，应该对检测和对照样品各进行至少5次复测检测。当计算出的复测次数超过5个时，应检测较多的复测次数。

对于双侧检验，假设测量误差呈正态分布，且试验样品和对照样品的重复性大致相等，所需的复测次数可由公式（1）计算得出[47-49]。

注：添加乘数2是为了考虑到两个正态分布的随机变量之差的SD。

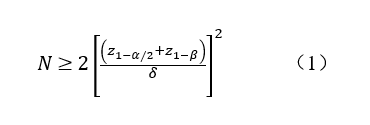
其中：

✔ z1-α/2是标准化正态分布中的100×（1-α/2）个百分点。

✔ z1-β是标准化正态分布的100×（1-β）百分位数。

✔ σ是在相关的质控品浓度下测量程序的假定重复性（运行内）SD，其依据是先前的知识，如生产厂家对精密度的要求、精密度研究的结果，或其他一些依据。

✔ δ是在要检测的被测量浓度下，由干扰引起的平均值之间的允许差异。这是最大的允许差异；任何大于此值的差异都被认为具有临床意义。

β的值应设置为等于0.20或更小，而α的值应设置为等于0.05或更小，从而确保统计功效至少为80%，假阳性率不超过5%。复测次数（N）需要是一个整数，所以N的计算值总是被四舍五入。

注：5%的假阳性率允许在使用复测20时平均不超过一个假阳性结果。

例如，评估者需要检测出1.5 mg/dL（或更大）的影响，这已被确定为可接受的干扰程度，在95%的置信水平（α = 0.05）和95%的统计功效（β = 0.05）下。这需要一个双侧检测。重复性的SD是1.0 mg/dL。为了计算所需的复测次数，使用公式（1）：

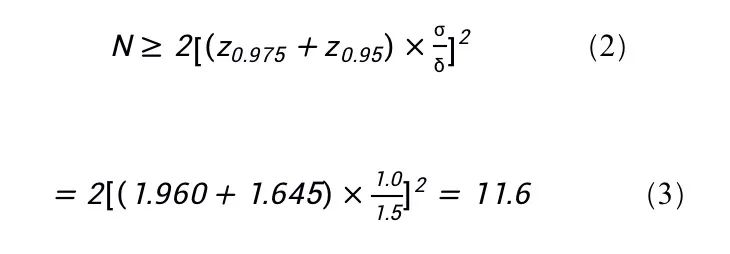
因为N需要是一个整数，所以这个数字总是被四舍五入的。因此，上例中每个样品（检测和对照）所需的复测次数为12。

对于单侧检验，将方程（1）中的z1-α/2替换为z1-α。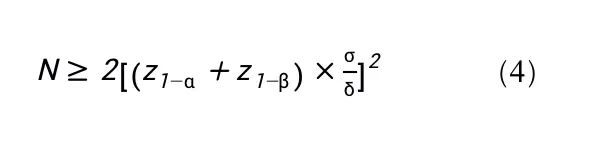

其中：

✔ z1-α是标准化正态分布的100×（1-α）百分位数，对应于单侧检验中错误地拒绝总体均值相等假设的第一类错误的概率α。

为方便起见，一些常用的置信水平和统计功效水平的Z值显示在表1中。

表1 | 常用的第一类和第二类错误的概率γ的z1-γ百分比

表2表示基础混样（NT）所需的最小复测次数和质控品（NC）所需的最小复测次数。基础混样和对照样品的最终复测次数不必相同，但至少应满足每个样品的最低要求。

表2中显示了在95%的置信水平和90%的统计功效下检测各种干扰效应所需的复测次数，即双侧检测。为方便起见，干扰标准以重复性（运行内）SD（δ/σ）的倍数表示。 

表2 | 检测各种干扰效应所需的复测次数，以5%的第一类错误概率和10%的第二类错误概率的双侧检验（90%的检验统计功效）

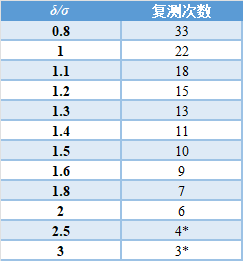
* 在这些情况下，至少需要复测五次和五次对照复测。

一个例子说明了足够数量的复测的重要性。在25 mIU/mL的情况下，假设检测的可重复性CV为5%。通过充分的复测，可以减少不精密度的影响，从而可以检测到7%的可能干扰。

为了确定在95%（α = 0.05）的置信水平和90%（β = 0.10）的统计功效下检测7%的干扰所需的复测次数，商（δ/σ）被表示为重复性的倍数，可以用偏倚超过SD或偏倚百分比超过CV%（例如，7%/5%=1.4）。

然后，使用表2来确定所需的复测次数，在本例中为11次。

当较大的干扰量被认为是可接受的，如10%的影响（δ/σ=2），则需要较少的复测。表2显示，在允许的干扰较大的情况下，控制和检测条件只需要6次复测，而不是11次。

好了，以上就是今天分享的全部内容，如果大家有什么疑问，欢迎在后台给我们留言，或者加入我们一起讨论，若觉得文章不错，也请关注我们，以免错过后续更新~